How to Tell if a Parabola Is Even or Odd

F x a x - h 2 k. It is clearly symmetric to the y axis and hence it is even.

Determine Whether A Function Is Even Odd Or Neither From Its Graph College Algebra

You can write y x 2 1 x 2 x 2 1 x 2 2 x 4 8 3 2 x 2 1 x 4 8 The approximation is the first three terms of the Taylor series near x 0.

. Its easiest to visually see even odd or neither when looking at a graph. Fxx2 f x x 2 square function in R R the calculation is fx x2 x2 fx f x x 2 x 2 f x so the square function fx f x is even. The parabola should be on a graph on a coordinate plane with x and y coordinatesStep 2 Remember the vertex form of a quadratic equation.

The mathematical definition of an even function is fx fx for any value of x. For a particular function to be odd the graph of that function must be symmetric about the origin. G -x dfrac 3 -x2 2 gx x2 23.

The sum of two odd functions is odd and any constant multiple of an odd function is odd. If the function has folded onto itself then it. We can see that the graph is symmetric to the origin.

The x 4 term spoils the parabola. Y f t displaystyle y f left tright y f t is said to be even if. See the animated illustration.

The only function that is even and odd is fx 0. In this video we look at the graph to determine if a given function is even odd or neither. A function is even if the graph of the function is symmetrical about the y-axis or a function is eve.

This is not a parabola. Thats the equation of only a parabola that opens up and has its vertex at 00. Graphically this involves that opposed.

This is a rational function. Learn how to determine if a function is even or odd. If a function is even the graph is symmetrical about the y-axis.

For example if you check the graph of y x 2 it is an upward parabola with its vertex at the origin. To see if a function is odd you can imagine folding the graph along its y-axis then along its x-axis or vice versa. Algebraically f is even if and only if f-x fx for all x in the domain of f.

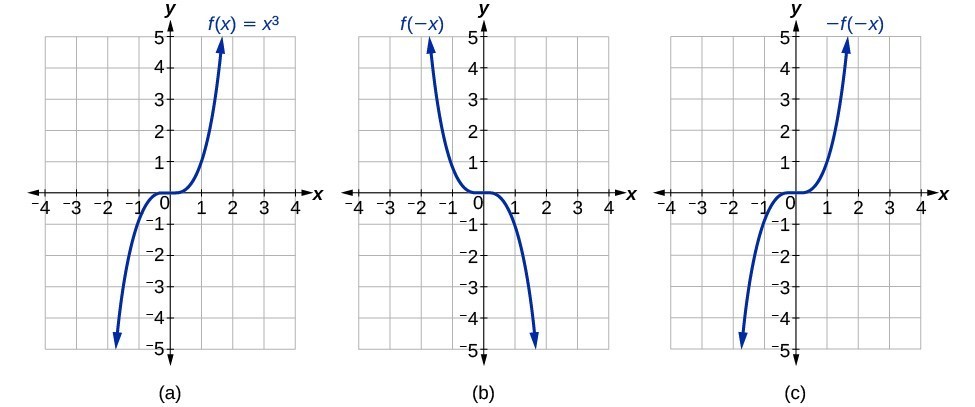
Determine whether the function satisfies latexfleftxrightfleft-xrightlatex. The a in the vertex form of a parabola corresponds to the a in standard form. The function graphed in question 4 is a parabola that opens down but its not an even function.

The graph of an even function is always symmetrical about the vertical axis that is we have a mirror image through the y -axis. Determine algebraically whether if the function is even odd or neither. An even function will provide an identical image for opposite values.

In this case we have a 2 which is positive and so we know that the parabola opens up. It is even if Log x-3 Log 3-x and odd if not. Basically the opposite input yields the.

Dfrac 3 x2 2 x223. The process for checking if its even odd or neither is the same as always. In general a parabola is the graph of a quadratic function of.

If a is negative the parabola will open downwards. You can verify using the formula f -x f x as well. The equation for parabolas that have openings facing the top and bottom use yaxh2kdisplaystyle yax-h2k.

Lets try another example of even odd neither. If you can remember the behavior for quadratics that is for parabolas then youll know the end-behavior for every even-degree polynomial. If the function has folded onto itself then it is even.

Next we need to find the x-intercepts. Step 1 Select the parabola that you want to use. These traits will be true for every even-degree polynomial.

Look again at the two graphs. That means we cut its graph along the y- axis and then reflect its even half in the x- axis first followed by the reflection in the y- axis. This means well need to solve an equation.

A parabola can either be even or it can be neither even nor odd but it cannot be odd. If the function is odd the graph is symmetrical about the origin. In vertex form hk describes the vertex of the parabola and.

Its an even function. Also to know is are parabolas even or odd. Given the formula for a function determine if the function is even odd or neither.

If a is positive the parabola will open upwards. But if the parabolas opening faces the left or right it. Also the vertex is a point below the x.

To see if a function is even you can imagine folding the graph along its y-axis. For example f3 9 and f3 9. Is even odd or neither.

Ill start by plugging x in for x. Follow this answer to receive notifications. F x f x f -x-f x f x f x the function is odd.

Determine whether the function is even or odd. 3 x 2 2. F t f t for all values of t.

The sum of two even functions is even and any constant multiple of an even function is even. Most functions will be neither even nor odd. Answered May 13 2017 at 526.

Fleft x right 3 x6 -. The simplest example of this is fx x 2 because fxf-x for all x. If it does it is even.

A function f is odd if the graph of f is symmetric with respect to the origin. I know equation of parabola is f xx 2. The product of two even functions is an even function.

Now lets look at some polynomials of odd degree cubics in the first row of pictures and quintics in the second row. However before we do that we can actually tell whether or not well have any before we even start to solve the equation. An even function is when fx f-x and an odd function is when the aforementioned statement is not true.

It is not too far from one. Determine whether the function satisfies latexfleftxright-fleft-xrightlatex. G x 3 x 2 2.

The Agony And Dx Dt End Behavior Of Polynomial Functions Polynomial Functions Studying Math Teaching Algebra

Even Odd Or Neither Functions The Easy Way Graphs Algebraically Properties Symmetry Youtube

Mfg The Vertex Of A Parabola